• -

TL;DR

How to sample variance ? Same as with mean, sample it heterogeneously = better deep neural networks for free.

Context

Learning representations of the world is learning about a continuum of values on an arbitrary space.

Learning images = learning representations of light (spaces = luminosity, contrast, colors, …) Learning sound = learning representation of air compression (spaces = frequency, amplitude, …)

If learning how to represent MNIST images, sampling every luminosity point is OK. Low number of pixels, low complexity problem.
This is sampling mean of distribution.

If learning how to representation real images, sampling mean of distribution not possible.
Complex distributions, mean is meaningless.

Solution one (top image below) : sample lots of mean. Precise but costly.
If representations ends up being same size as input, process useless.

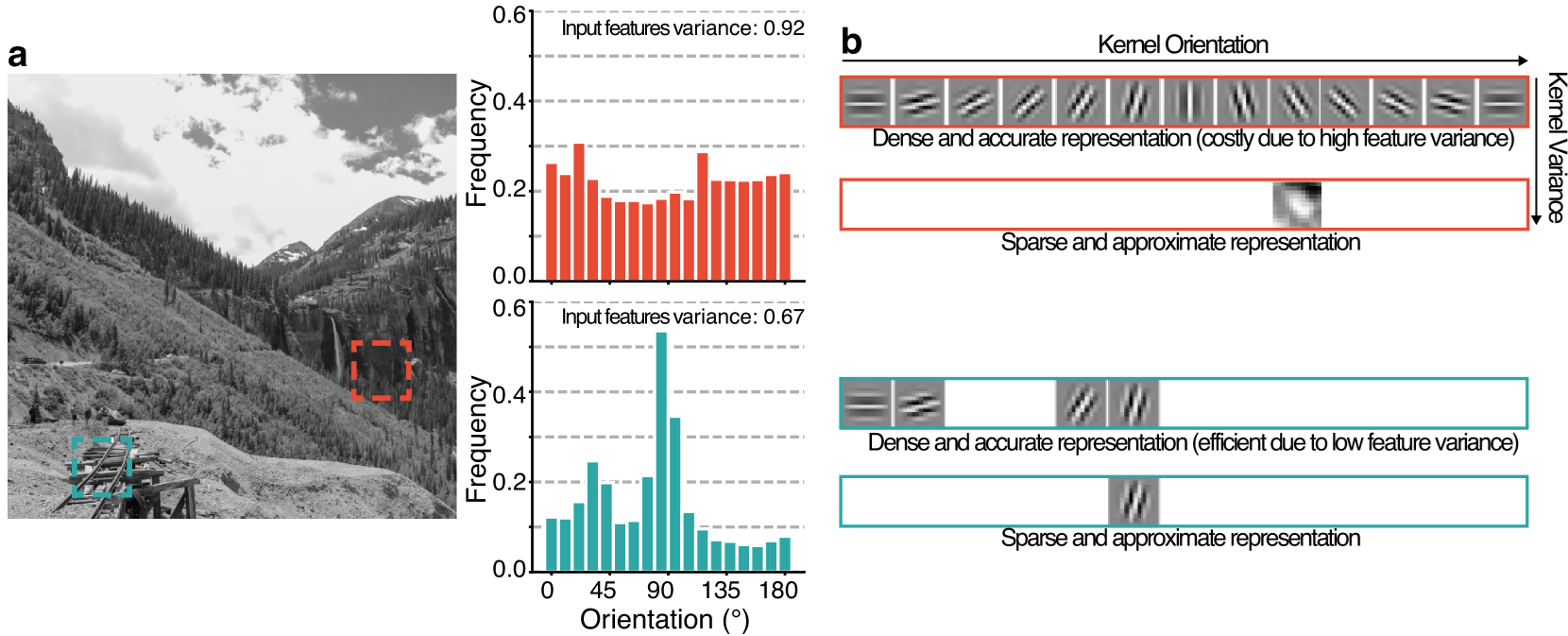
Solution two (bottom image above) : sample mean, describe succintly variance around it. Approximative, but efficient.
Useful, also gives idea of how much one bit of information varies with respect to others.

Natural images

For the problem of natural images, sampling variance very useful. Stereotypical pattern of distribution of orientations.

Learning from this

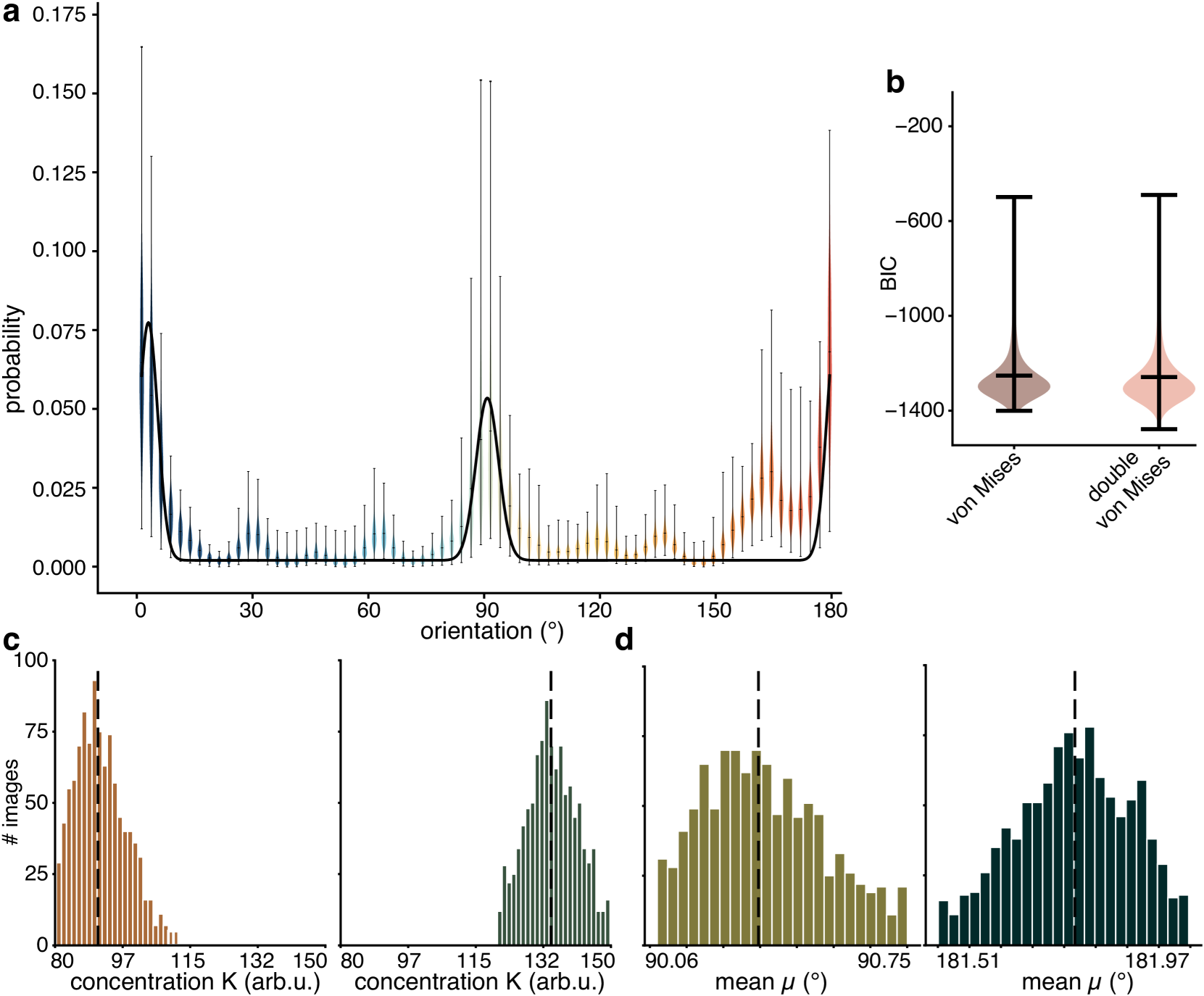
If one tries to make models of these images (here, sparse coding), good models also get this distribution of orientations.

Logical step : already give this distribution to the models. Save them time from figuring it out.
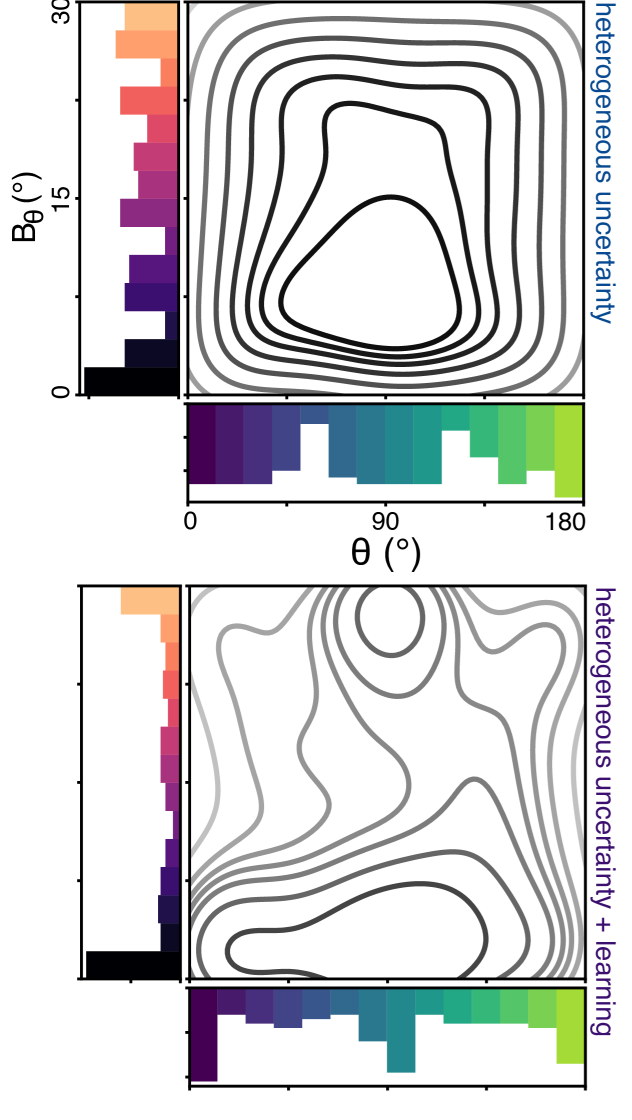
5 scenarii :

• green = sample only mean (same uncertainty/variance sampling in the model)
• blue = sample mean and variance (heterogeneous variance sampling)
• orange = green + fine tuning on dataset
• purple = blue + fine tuning on dataset
• black = let the model learn everything (fine tuning on the dataset, without any intervention)

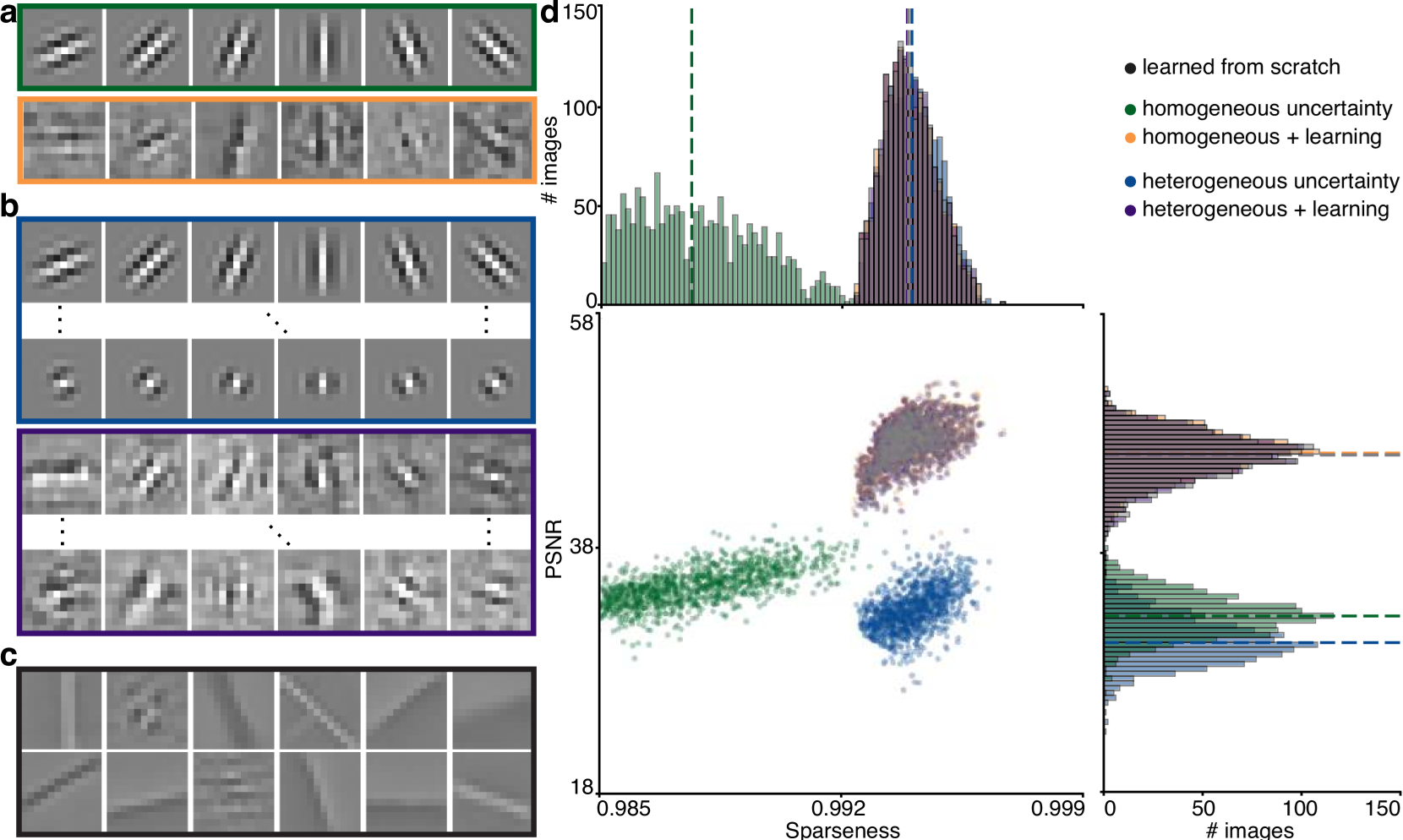
Learning always gives best representation quality (Peak Signal to Noise Ratio, PSNR) and efficiency (sparseness).
Without learning, sampling variance massively boosts sparseness. Slight cost in quality.

Learning = finding the best of both worlds ! Simple task of reconstruction, no big difference.

Complex task ? Put that into a deep neural network that classifies images.

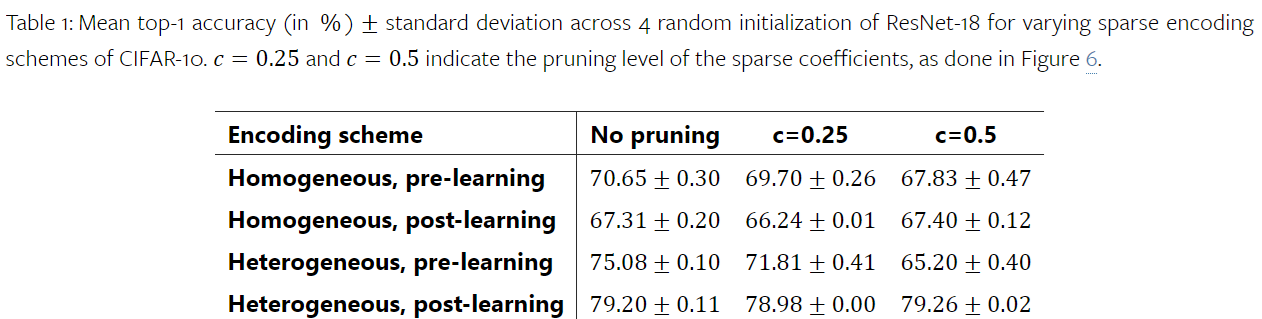
Sampling variance (last row, first column) much better for representations.

Sampling variance (last row, second and third column) also much, much better than others methods when facing noise.
Here, cutting off a fraction of the coefficients (25% or 50%) does not significantly hinder the model. Performance collapses for other.

Relevance

In previous paper (Cortical recurrence something something sensory variance), showed that neurons in actual brain compute variance.
Here, showed that this computation is very useful. Namely, prevents models from failing when facing noise. Important for brain, noisy machines !

Full code in PyTorch - seamlessly integrate this into any deep neural network !

On a personal note

Talked myself into buying a new GPU for this paper.
Now mostly used for Cyberpunk 2077, rather than PyTorch.